[백준] 1937 욕심쟁이 판다 c++

문제 링크 https://www.acmicpc.net/problem/1937

문제

n × n의 크기의 대나무 숲이 있다. 욕심쟁이 판다는 어떤 지역에서 대나무를 먹기 시작한다. 그리고 그 곳의 대나무를 다 먹어 치우면 상, 하, 좌, 우 중 한 곳으로 이동을 한다. 그리고 또 그곳에서 대나무를 먹는다. 그런데 단 조건이 있다. 이 판다는 매우 욕심이 많아서 대나무를 먹고 자리를 옮기면 그 옮긴 지역에 그 전 지역보다 대나무가 많이 있어야 한다.

이 판다의 사육사는 이런 판다를 대나무 숲에 풀어 놓아야 하는데, 어떤 지점에 처음에 풀어 놓아야 하고, 어떤 곳으로 이동을 시켜야 판다가 최대한 많은 칸을 방문할 수 있는지 고민에 빠져 있다. 우리의 임무는 이 사육사를 도와주는 것이다. n × n 크기의 대나무 숲이 주어져 있을 때, 이 판다가 최대한 많은 칸을 이동하려면 어떤 경로를 통하여 움직여야 하는지 구하여라.

입력

첫째 줄에 대나무 숲의 크기 n(1 ≤ n ≤ 500)이 주어진다. 그리고 둘째 줄부터 n+1번째 줄까지 대나무 숲의 정보가 주어진다. 대나무 숲의 정보는 공백을 사이로 두고 각 지역의 대나무의 양이 정수 값으로 주어진다. 대나무의 양은 1,000,000보다 작거나 같은 자연수이다.

출력

첫째 줄에는 판다가 이동할 수 있는 칸의 수의 최댓값을 출력한다.

풀이 과정

처음에는 단순하게 DFS 재귀를 이용하여 구현했다. 하지만, DP를 사용하지 않으면 시간초과가 났다. 괜히 골드3 문제가 아니다. DP와 DFS를 같이 사용해야 하는 새로운 문제 유형이었다.

우선, dp[a][b] = c는 “판다가 (a, b)에 있을 때 최대로 살 수 있는 날 수는 c일이다.”를 의미한다.

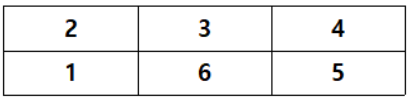
만약 이 그림 (0, 0)에 판다를 냅둔다면, (0, 0) -> (0, 1) -> (0, 2) -> (1, 2) -> (1, 1) 을 통해서 총 5일을 살게 될 것이다. 그럼 dp[0][0] = 5, dp[0][1] = 4, dp[0][2] = 3, dp[1][2] = 2, dp[1][1] = 1로 배열 값이 설정된다.
이후에 (1, 0)을 방문했다고 생각하고, (0, 0)으로 움직인다면 이미 5 값을 가지고 있기 때문에 방문을 해봤자, 결과는 5가 나오게 될 것이다. 즉, 이미 값이 있는 좌표는 방문을 더 이상 할 필요가 없다.

따라서, 재귀를 호출하는 과정에서 dp[][]에 값이 있는 좌표라면 그대로 해당좌표의 dp[][] 값을 return 해주면 된다. 그게 아니라면, 해당 좌표를 1로 두고 탐색을 진행한다.

아직 dfs에 익숙하지 않아서 직접 재귀를 그려봤다.

DP + DFS (AC)

#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;

int n, ans;
int num[501][501];
int dp[501][501];

int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, -1, 0, 1 };

int dfs(int x, int y) {
	if (dp[x][y]) return dp[x][y];
	dp[x][y] = 1;

	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];

		if (nx < 1 || nx > n || ny < 1 || ny > n)
			continue;
		if (num[x][y] < num[nx][ny]) {
			dp[x][y] = max(dp[x][y], dfs(nx, ny) + 1);
		}
	}
	return dp[x][y];
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> num[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			ans = max(ans, dfs(i, j));
		}
	}
	cout << ans;
}

처음 시도해봤던 시간초과나는 코드….! DFS (TLE)

#include <vector>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <stack>
#include <queue>
#include <string>
#define _CRT_SECURE_NO_WARNINGS
#pragma warning(disable : 4996)
using namespace std;

int n, ans;
int num[501][501];
bool c[501][501];

int dx[4] = { 1, 0, -1, 0 };
int dy[4] = { 0, -1, 0, 1 };

void dfs(int x, int y, int cnt) {
	c[x][y] = 1;
	ans = max(ans, cnt);

	for (int i = 0; i < 4; i++) {
		int nx = x + dx[i];
		int ny = y + dy[i];

		if (nx < 1 || nx > n || ny < 1 || ny > n)
			continue;
		if (num[x][y] < num[nx][ny] && !c[nx][ny]) {
			c[nx][ny] = 1;
			dfs(nx, ny, cnt + 1);
			c[nx][ny] = 0;
		}
	}
}

int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL); cout.tie(NULL);

	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> num[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			dfs(i, j, 1);
			memset(c, 0, sizeof(c));
		}
	}
	cout << ans;
}